Example code producing the bug:

from quantities import C, N, m, A, mm, V, F, \
  pF, H, ohm, Hz, MHz, S, s, kg, mS, rad
import numpy as np
from numpy import pi, exp

epsilon0 = 8.854187817 * 10**(-12) * C**2/(N*m**2)
mu0 = 4*pi*10**(-7) * N/(A**2)

def R_outer(r_center, Z_0, epsilonr):
  epsilon  = epsilon0*epsilonr
  return r_center*(exp(2*pi*Z_0/np.sqrt(mu0/epsilon)) - 1)

Z_0 = 75*ohm
r_center = 0.6*mm
R_outer(r_center, Z_0, 2.25)

Running that code gives this error:

If I print out the expression inside the exp function, I get this:

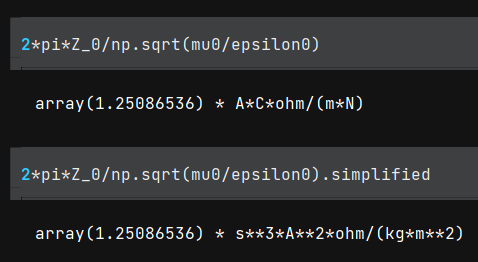
The issue seems to be that it's treating ohm as if it were a base SI unit, rather than splitting it up into the base units and cancelling out common units, as it did for Coulombs and Newtons, and as the documentation for the simplify method says it should. It's easy to check that all those units do in fact cancel out by rewriting ohms in base units.